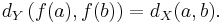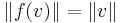Isometry

For the mechanical engineering and architecture usage, see isometric projection. For isometry in differential geometry, see isometry (Riemannian geometry).

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.

Isometries are often used in constructions where one space is embedded in another space. For instance, the completion of a metric space M involves an isometry from M into M', a quotient set of the space of Cauchy sequences on M. The original space M is thus isometrically isomorphic to a subspace of a complete metric space, and it is usually identified with this subspace. Other embedding constructions show that every metric space is isometrically isomorphic to a closed subset of some normed vector space and that every complete metric space is isometrically isomorphic to a closed subset of some Banach space.

An isometric surjective linear operator on a Hilbert space is called a unitary operator.

1 Definitions
2 Examples
3 Linear isometry
4 Generalizations
5 See also
6 References

Definitions

The notion of isometry comes in two main flavors: global isometry and a weaker notion path isometry or arcwise isometry. Both are often called just isometry and one should determine from context which one is intended.

Let X and Y be metric spaces with metrics d_X and d_Y. A map ƒ : X → Y is called an isometry or distance preserving if for any a,b ∈ X one has

$d_Y\left(f(a),f(b)\right)=d_X(a,b).$

An isometry is automatically injective. Clearly, every isometry between metric spaces is a topological embedding.

A global isometry, isometric isomorphism or congruence mapping is a bijective isometry.

Two metric spaces X and Y are called isometric if there is a bijective isometry from X to Y. The set of bijective isometries from a metric space to itself forms a group with respect to function composition, called the isometry group.

There is also the weaker notion of path isometry or arcwise isometry:

A path isometry or arcwise isometry is a map which preserves the lengths of curves (not necessarily bijective).

This is often called just isometry and one should determine from context which one is intended.

Examples

Any reflection, translation and rotation is a global isometry on Euclidean spaces. See also Euclidean group.

The map R 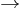$\to$ R defined by 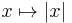$x\mapsto |x|$ is a path isometry but not an isometry.

The isometric linear maps from Cⁿ to itself are the unitary matrices.

Linear isometry

Given two normed vector spaces V and W, a linear isometry is a linear map f : V → W that preserves the norms:

$\|f(v)\| = \|v\|$

for all v in V. Linear isometries are distance-preserving maps in the above sense. They are global isometries if and only if they are surjective.

By the Mazur-Ulam theorem, any isometry of normed vector spaces over R is affine.

Generalizations

Given a positive real number ε, an ε-isometry or almost isometry (also called a Hausdorff approximation) is a map 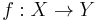between metric spaces such that
1. for x,x′ ∈ X one has |d_Y(ƒ(x),ƒ(x′))−d_X(x,x′)| < ε, and
2. for any point y ∈ Y there exists a point x ∈ X with d_Y(y,ƒ(x)) < ε

That is, an ε-isometry preserves distances to within ε and leaves no element of the codomain further than ε away from the image of an element of the domain. Note that ε-isometries are not assumed to be continuous.

Quasi-isometry is yet another useful generalization.

References

F. S. Beckman and D. A. Quarles, Jr., On isometries of Euclidean space, Proc. Amer. Math. Soc., 4 (1953) 810-815.